فرار از ماتریس

اختصاصی از زد فایل فرار از ماتریس دانلود با لینک مستقیم و پر سرعت .

دانلود تحقیق نمایش های مختلف ماتریس اسپارس و کاربرد آن در پردازش تصویر

اختصاصی از زد فایل دانلود تحقیق نمایش های مختلف ماتریس اسپارس و کاربرد آن در پردازش تصویر دانلود با لینک مستقیم و پر سرعت .

توجه و روی آوردن به روش های پردازش تصاویر به اوایل سال 1920 باز می گردد، زمانی که عکس های دیجیتال برای اولین بار توسط کابل های زیردریایی از نیویورک به لندن فرستاده شد.با این حال، کاربرد مفهوم پردازش تصویر تا اواسط 1960 گسترش وپیشرفت چندانی نیافت. در  1960 بود که کامپیوتر های نسل سوم دیجیتال به بازار آمد که می توانست سرعت و حافظه بالای مورد نیاز برای پیاده سازی الگوریتم های پردازش تصویر رافراهم کند.

از آن پس، تجربه در این زمینه گسترش یافت. مطالعات و تحقیقات زیادی در این موضوع در علوم مختلف از جمله : مهندسی،  علوم کامپیوتر، علوم اطلاعات، فیزیک، شیمی، بیولوژی و داروسازی انجام شد.

نتیجه ی این تلاش ها در تکنیک های پردازش تصویر در مسائل مختلف - از بهبود کیفیت و بازیابی تصاویر گرفته تا پردازش اثر انگشت در مسائل تجاری – خود رانشان داد.

در این فصل بر آنیم که تکنیک ها و روش های مختلف پردازش تصویر را معرفی و بررسی کنیم. اما پیش از پرداختن به روش ها ، برخی تعاریف پایه را ذکر خواهیم کرد.

1-1 تصویر دیجیتالی:

تصویر به عنوان ترجمه image نشانگر یک شکل دو بعدی می باشد که توسط یک وسیله ی حساس به نور مانند دوربین به وجود آمده باشد. اما picture (عکس) نشانگر هر گونه شکل دو بعدی مانند یک تابلوی نقاشی و یا یک دست نوشته است. مقصود از تصویر دیجیتال ، digital image می باشد.

یک تصویر را می توان توسط تابع دوبعدی f(x,y) نشان داد که در آن x و y را مختصات مکانی و مقدار f در هر نقطه را شدت روشنایی تصویر درآن نقطه می نامند. اصطلاح سطح خاکستری نیز به شدت روشنایی تصاویر مونوکروم (monochrome)  اطلاق میشود . تصاویر رنگی نیز از تعدادی تصویر دوبعدی تشکیل می شود.

 زمانی که مقادیر x و y و مقدار f(x,y) با مقادیر گسسته و محدود بیان شوند ، تصویر را یک تصویر دیجیتالی می نامند. دیجیتال کردن مقادیر x و y را Sampling و دیجیتال کردن مقدار f(x,y) را quantization گویند.

 برای نمایش یک تصویر M * N از یک آرایه دو بعدی ( ماتریس) که M سطر و N ستون دارد استفاده می کنیم . مقدار هر عنصر از آرایه نشان دهنده ی شدت روشنایی تصویر در آن نقطه است. در تمام توابعی که پیاده سازی می شود ، هر عنصر آرایه یک مقدار 8 بیتی است که می تواند مقداری بین 0 و 255 داشته باشد. مقدار صفر نشان دهنده ی رنگ تیره   ( سیاه ) و مقدار 255 نشان دهنده رنگ روشن ( سفید ) است.

به عنوان مثال تصویر زیر که سایز آن 265×288 است از یک ماتریس که دارای 288 سطر و 265 ستون است برای نمایش تصویر استفاده می کند

هر پیکسل از این تصویر نیز مقداری بین 0 و 255 دارد . نقاط روشن مقادیری نزدیک به 255 و نقاط تیره مقادیر نزدیک به 0 دارد. همه ی توابع پردازش تصویر از این مقادیر استفاده کرده و اعمال لازم را بر روی تصویر انجام می دهند.

2-1 تعریف رنگ و ویژگی های آن:

برای ارایه ی یک تعریف صحیح از رنگ باید علاوه بر پدیده های فیزیکی و قوانین حاکم بر آن، نتیجه ی حاصل از این پدیده های فیزیکی که ذهنی می باشد را نیز در نظر گرفت.

از دیدگاه فیزیکی ایجاد رنگ به 3 عامل بستگی دارد که عبارتند از :

1)منبع نوری که جسم را روشن می کند.

2)جسم که به وسیله منع نوری روشن می شود.

3)چشم و مغز که رنگ را دریافت می کند.

اگرچه بهترین دریافت کننده ای که می تواند رنگ را بسنجد و در مورد آن دریک لحظه قضاوت نماید چشم و مغز انسان می باشد، اما به جز چشم نور یاب های دیگری مانند فتو تیوپها و فتوسلها نیز در سنجش  رنگ  توسط دستگاه ها  به کار می روند. جهت ایجاد رنگ های متفاوت، منبع نوری باید علاوه بر انرژی مناسب، توزیع کافی در طیف مریی بین 380 تا 760 نانومتر را داشته باشد و مشاهده کننده نیز از بینایی رنگی معمول و نرمالی برخوردار باشد. به علاوه محیط مشاهده نیز از فضای مناسبی برای تشخیص جسم برخوردار باشد.

بدیهی است که با تغییر هر یک از سه عامل اصلی ایجاد کننده ی رنگ یعنی منبع نوری، جسم و مشاهده کننده تغییراتی دررنگ ظاهر شده ایجاد خواهد شد.

به سیستم هایی که بیان و تنظیم رنگ را  ارایه می دهند " فضای رنگ " گویند. در ادامه به تعریف چند سیستم فضای رنگ رایج می پردازیم.

1-2-1 فضای رنگ HSV :

به منظور بررسی  رفتار یک انسان در موردرنگ و تقسیم بندی آنان فرض می گردد که شخصی که هیچ تجربه قبلی راجع به رنگ ندارد قصد دارد سنگ هایی با رنگ های مختلف را طبقه بندی نموده و از لحاظ رنگ آن ها را منظم و نامگذاری نماید. فرض می شود اولین کار شخص جدا کردن سنگ های رنگی از سنگ های غیر رنگی مانند سیاه و سفید و خاکستری باشد.

در میان سنگ های غیر رنگی می توان ردیف منطقی از رنگ های سفید و خاکستری روشن و خاکستری تیره  و سیاه ایجاد نمود و یا به عبارت دیگر در میزان روشنایی آن ها تفکیک قایل شد. نام دیگر آن کیفیت ارزش*  می باشد.

شامل 85 صفحه فایل word قابل ویرایش

تحقیق در مورد مدل ها و استراتژی های ماتریس

اختصاصی از زد فایل تحقیق در مورد مدل ها و استراتژی های ماتریس دانلود با لینک مستقیم و پر سرعت .

لینک پرداخت و دانلود *پایین صفحه*

فرمت فایل : Word(قابل ویرایش و آماده پرینت)

تعداد صفحه : 38

فهرست مطالب:

مقدمه

مدلها و استراتژی ماتریس

ارزیابی عملکرد

مدل سینک و تاتل (1989)

ماتریس عملکرد (1989)

مدل نتایج و تعیین کننده ها (1991)

هرم عملکرد (1991)

کارت امتیازدهی متوازن (1992)

مدل ماتریس استراتژی اصلی

مدل ماتریس پورت فولیو

ویژگیهای ماتریس های پورت فولیو

ماتریس داخلی و خارجی

مدل گروه مشاوره ای بوستون 4(ماتریس BCG )

مدل شرکت جنرال الکتریک (GE):

ماتریس تهدیدات، فرصت ها، نقاط قوت و نقاط ضعف( SWOT)

ماتریس داخلی و خارجی (IE) (4)

ماتریس ارزیابی موقعیت و اقدام استراتژیک (Space)11

ماتریس داخلی و خارجی ( IE )

ماتریس BCG و GE

ماتریـس کاتـلر و آنسـوف

مقدمه

فقدان ساختار علمی در انتقال استراتژی‌های تدوین شده به سطوح تصمیم‌گیری پایین سازمان، باعث بروز مسائلی در بخش صنایع تولیدی می‌شود. ادبیات استراتژی‌های آکادمیک، بیانگر مفاهیم و روش‌های تدوین استراتژی‌ها از دیدگاه بازار است، در حالی که بین تدوین استراتژی‌ها و اجرای آنها، اغلب شکافی آشکار بروز می‌کند. هدف مقاله حاضر، ارائه نوعی مدل تصمیم‌گیری است که بین مفاهیم استراتژی‌های تولیدی و تصمیم‌گیری‌های استراتژیک، مطابق با اصول جریان سیستم‌های تولیدی، ارتباط برقرار کند. نتیجه مقاله، بیانگر انتقال استراتژی‌ها از سطوح تصمیمات استراتژیک به سطوح تصمیم‌گیری براساس اصول جریان زیرسیستم‌هاست.

براساس تحقیقات آکادمیک انجام شده، الگوی تصمیم‌گیری‌های استراتژیک می‌بایستی در حوزه‌های مختلف و براساس فرایند تدوین استراتژی‌های تولید، ایجاد شود. در دیدگاه بالا به پایین، تصمیمات استراتژیک براساس موقعیت کسب و کار و محیط بازار، اتخاذ می‌شوند. روش هدایت مدیریت از طریق تدوین استراتژی، مستلزم تلاش فراوان است. در عین حال، بسیاری از شرکت‌ها دارای روشی ساختارمند برای برقراری ارتباط و اجرای استراتژی‌های خود نیستند. به منظور دستیابی به موفقیت در دنیای واقعی، ایجاد مدلی برای پشتیبانی از اجرای استراتژی‌ها در عمل، از اهمیت خاصی برخوردار است. هدف از ارائه این مدل تصمیم‌گیری، هدایت استراتژی‌های تولیدی به تصمیمات استراتژیک مبتنی‌بر اصول جریان سیستم‌های تولیدی در سطوح زیر سیستم‌های کارخانه است. این دیدگاه، محدود به طراحی سیستم‌های تولیدی و برنامه‌ریزی و کنترل تولید است.با توجه به اینکه محتوای استراتژی‌های تولیدی در طراحی سیستم‌های تولیدی و برنامه‌ریزی و کنترل تولید نمایان می‌باشد، این مقاله، بیانگر مدلی کاربردی در تصمیم‌گیری‌های استراتژیک در ارتباط با جریان سیستم‌های تولیدی است.به دلیل فقدان مدل‌های تصمیم‌گیری، نیاز مدیران به تصمیم‌گیری‌های استراتژیک و تنظیم استانداردهای عملکرد مرتبط با جریان سیستم‌های تولیدی، وجود مدلی جامع ضروری به نظر می‌رسد. این مدل، براساس مصاحبه‌ها، بررسی‌ها و مطالعات گسترده، ایجاد و اصلاح شده و گامی است که اجرا و هدایت آن ضروری است.

آموزش متلب، جزوه آموزش محاسبه معکوس ماتریس با استفاده از کوفاکتور Cofactor در نرم افزار MATLAB

اختصاصی از زد فایل آموزش متلب، جزوه آموزش محاسبه معکوس ماتریس با استفاده از کوفاکتور Cofactor در نرم افزار MATLAB دانلود با لینک مستقیم و پر سرعت .

 

در جبر خطی کوفاکتور (یا گاهی مکمل”adjunct”) به ساختاری گفته می شود که هم در محاسبه دترمینان و هم در محاسبه معکوس یک ماتریس مربعی کاربرد دارد. بطور خاص برای هر عضو (i,j) در یک ماتریس مربعی یک عدد بنام کوفاکتور (i,j) محاسبه می گردد که در ماتریسی با نام کوفاکتور برای محاسبه ی معکوس ماتریس مربعی مورد استفاده قرار می گیرد.

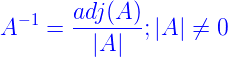
جزوه آموزش محاسبه معکوس ماتریس با استفاده از کوفاکتور Cofactor در نرم افزار MATLAB، حاوی برنامه MATLAB برای کوفاکتور نوشته شده می باشد و با دریافت ماتریس ورودی A ماتریس کوفاکتور را برای یک ماتریس مربعی n x n تولید می نماید و با استفاده از رابطه بالا معکوس ماتریس ورودی A را محاسبه می نماید adj (A ترانهاده ماتریس کوفاکتور است). نهایتا برنامه در خروجی ماتریس کوفاکتور و ماتریس معکوس A را نمایش خواهد داد.

همچنین به همراه فایل جزوه بالا m فایل استفاده شده در این جزوه آموزشی، در فایل rar دانلود شده موجود می باشد. این جزوه مشتمل بر 6 صفحه، به زبان انگلیسی، تایپ شده، با فرمت PDF، گردآوری شده است.

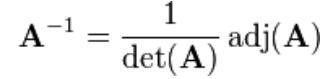
جهت خرید جزوه آموزش محاسبه معکوس ماتریس با استفاده از کوفاکتور Cofactor در نرم افزار MATLAB، به مبلغ فقط 3000 تومان و دانلود آن بر لینک پرداخت و دانلود در پنجره زیر کلیک نمایید.

!!لطفا قبل از خرید از فرشگاه اینترنتی کتیا طراح برتر قیمت محصولات ما را با سایر فروشگاه ها و محصولات آن ها مقایسه نمایید!!

!!!تخفیف ویژه برای کاربران ویژه!!!

با خرید حداقل 20000 (بیست هزارتومان) از محصولات فروشگاه اینترنتی کتیا طراح برتر برای شما کد تخفیف ارسال خواهد شد. با داشتن این کد از این پس می توانید سایر محصولات فروشگاه را با 20% تخفیف خریداری نمایید. کافی است پس از انجام 20000 تومان خرید موفق عبارت درخواست کد تخفیف، شماره همراه و ایمیلی که موقع خرید ثبت نمودید را به ایمیل فروشگاه ([e-mail]) ارسال نمایید. همکاران ما پس از بررسی درخواست، کد تخفیف را به ایمیل شما ارسال خواهند نمود.

تحقیق در مورد اشنایی با ماتریس

اختصاصی از زد فایل تحقیق در مورد اشنایی با ماتریس دانلود با لینک مستقیم و پر سرعت .

ک پرداخت و دانلود *پایین مطلب*

فرمت فایل:Word (قابل ویرایش و آماده پرینت)

تعداد صفحه:27

فهرست مطالب ندارد

آشنایی با ماتریسها

مقدمه: آشنایی با ماتریسها

مقدمه: در تاریع آمده است که اولین بار یک ریاضیدان انگلیسی تبار به نام کیلی ماتریس را در ریاضیات وارد کرد. با توجه به آنکه در آن زمان ریاضیدانان اغلب به دنبال مسائل کاربردی بودند، کسی توجهی به آن نکرد. اما بعدها ریاضیدانان دنباله ی کار را گرفتند تا به امروز رسید که بدون اغراق می توان گفت در هر علمی به گونه ای با ماتریس ها سروکار دارند. یکی از نقش های اصلی ماتریس ها آن است که آنها ابزار اساسی محاسبات عملی ریاضیات امروز هستند، درست همان نقشی که سابقاً اعداد بر عهده داشتند. از این نظر می توان گفت نقش امروز ماتریس ها همانند نقش دیروز اعداد است. البته، ماتریس ها به معنایی اعداد و بردارها را در بر دارند، بنابراین می توان آنها را تعمیمی از اعداد و بردارها در نظر گرفت. در ریاضیات کاربردی ماتریس ها از ابزار روز مره هستند، زیرا ماتریس ها با حل دستگاه معادلات خطی ارتباط تنگاتنگی دارند و برای حل ریاضی مسائل عملی، مناسبترین تکنیک، فرمول بندی مسئله و یا تقریب زدن جوابهای مسئله با دستگاه معادلات خطی است که در نتیجه ماتریس ها وارد کار می شوند. اما، مشکلی اصلی در ریاضیات کابردی این است که ماتریس های ایجاد شده، بسیار بزرگ هستند و مسئله اصلی در آنجا کار کردن با ماتریس های بزرگ است. از جنبه نظری، فیزیک امروزی که فیزیک کوانتوم است، بدون ماتریس ها نمی توانست به وجود آید. هایزنبرگ – اولین کسی که در فیزیک مفاهیم ماتریس ها را به کار برد- اعلام کرد «تنها ابزار ریاضی که من در مکانیک کوانتوم به آن احتیاج دارم ماتریس است.» بسیاری از جبرها مانند جبر اعداد مختلط و جبر بردارها را با ماتریس ها بسیار ساده می توان بیان کرد. بنابراین با مطالعه ماتریسها، در واقع یکی از مفیدترین و در عین حال جالبترین مباحث ریاضی مورد بررسی قرار می گیرد.

تعریف ماتریس: اگر بخواهیم مانند کیلی، ماتریس را تعریف کنیم، باید گفت هر جدول مستطیلی که دارای تعداد سطر و ستون است و در هر خانه آن یک عدد وجود دارد یک ماتریس است. به عبارت دیگر هر آرایشی از اعداد مانند مثالهای زیر را ماتریس می گویند.

اگر ماتـریس      را A بنامیـم، در این صورت ماتـریس ] 15و10 و 1-[ را سطـر اول و ] 19و7 و5[ را سطر دوم و ،     ،    را به ترتیب ستون اول، ستون دوم، ستون سوم A گویند. ماتریس A را که دارای دو سطر و ستون است یک ماتریس دو در سه (2و3) می گویند. اصطلاحاً می گوییم A از مرتبه 2 در 3 است. (نوشته می شود 3×2). بنابراین ماتریس ] 7و5 و12[ B= یک ماتریس 4×1 و ماتریس C یک ماتریس 3×3 است.

به اعداد یا اشیاء واقع در جدول ماتریس درایه های آن ماتریس می گویند. درایه های هر ماتریس در جا ومکان مشخصی قرار دارند. مثلاً در ماتریس درایه 3 در سطر اول و ستون اول است. همچنین درایه سطر دوم، ستون سوم عدد 6 است. به طور کلی اگر درایه های سطر I ام ستون jام را با aij نشان دهیم؛ داریم

… و 5=12a   2=22a    3=11a

به طور کلی یک ماتریس دلخواه 3×2 را بصورت زیر نمایش می دهیم:

اغلب برای سهولت، به جای نمایش ماتریس به صورت فوق، آن را با نماد 3*2[aij]نشان می دهند که در آن aij را درایه یا عنصر عمومی ماتریس 3*2[aij] گویند. به طور کلی برای ساختن انواعی از ماتریس های دیگر می توانیم به جای آن که درایه های ماتریس را از اعداد حقیقی انتخاب کنیم، درایه ها را از اعداد مختلط عناصر یک میدان، توابع و یاحتی ماتریس ها انتخاب کنیم.

در حالت کلی یک ماتریس m*n بصورت A=[aij]m*n عبارت است از:

ماتریس های مربع: اگر در یک ماتریس تعداد سطرها و ستون ها مساوی باشد، آن را ماتریس مربع گویند. در این حالت اگر یک ماتریس مانند A دارای مرتبه ی n*n باشد، گوییم A یک ماتریس مربع مرتبه n است. مجموعه ماتریس های مربع مرتبه ی n را با     یا   نشان می دهند.

درایه های 11a و 22a و… و anx یک ماتریس مربع مرتبه n باشد، مجموع درایه های قطر اصلی A را اثر ماتریس A می نامند و با نماد tr(A) نشان می دهند. بنابراین:

در واقع اثر ماتریس، تابعی از مجموعه ماتریسهای مربع در مجموعه اعداد حقیقی است، یعنی

مثال: اگر      درایه های قطر اصلی A عبارتند از 4- و 6- بنابراین

2=6+4-tr(A)

ماتریس سطری: ماتریس هایی را که فقط یک سطر دارند ماتریس سطری یا بردار سطری می نامند. مثلاً ماتریس ی ماتریس سطری *n1 است.

ماتریس ستونی: ماتریسی است که فقط دارای یک ستون باشد. هر ماتریس ستونی را بردار ستونی نیز می گویند. مثلاً ماتریس زیر یک ماتریس ستونی 1×m است.

ماتریس صفر: ماتریسی است که همه درایه هایش صفر باشد. بنابراین ماتریس   ماتریس صفر است. هرگاه:

ماتریس صفر از مرتبه m*n را با نماد Qm*n نشان می دهند.

مثال:

اگر مرتبه ماتریس صفر، داده شده باشد و یا از طریق متن، مرتبه آن معلوم باشد، در اینصورت برای سهولت ماتریس صفر را با و یا حتی با O نشان می دهند.

تساوی ماتریس ها: هرگاه در ریاضیات اشیا جدیدی معرفی شوند، باید مشخص شوند که چه وقت دوتای آنها با هم مساویند. مثلاً در مجموعه اعداد گویا دو عدد دو سوم و چهار ششم را، علیرغم اینکه یک شکل نیستند، مساوی می نامند. در مورد اعدادگ ویا، دو عدد       را مساوی می گویند. هر گاه ad=bc تساوی ماتریسها نیز به صورت زیر تعریف می شود.

تعریف: دو ماتریس و   مساویند هرگاه هم مرتبه باشند و درایه های نظیر در دو ماتریس (یعنی درایه های هم موضع) مساوی باشند. به عبارت دیگر، دو ماتریس    و   مساویند هر گاه داشته باشیم:

مثال:      و   تساوی A و B به این معناست که

جمع ماتریس ها: مجموع دو ماتریس   و   ماتریسی است که با نماد A+B نشان می دهیم و به صورت زیر تعریفق می شود.

توجه کنید که برای جمع دو ماتریس می بایست دو ماتریس هم مرتبه باشند. بنا به تعریف اگر A+B+C=[Cij] در اینصورت

برای این که تعریف فوق روشن تر شود، شکل گسترده آن را در حالت ماتریس های 2×2 در زیر می آوریم

تذکر: با توجه به تعریف، جمع دو ماتریس A+B وقتی تعریف شده که A و B هم مرتبه باشند. در این صورت A و B را ماتریس های قابل جمع می گویند.

تعبیر عمل جمع دو ماتریس به مثابه یک ماشین: عمل جمع را می توان به منزله ماشینی تصور کرد که دارای دو ورودی و یک خروجی است (مطابق شکل)، به طوری که اگر دوماتریس مثلا2×2 به آن بدهیم از خروجی آن یک ماتریس 2×2 بیرون می اید.

قرینه یک ماتریس: اگر A یک ماتریس m*n باشد، قرینه A ماتریسی است از همان مرتبه که با نماد –A نشان می دهند و اگر    در این صورت بنا به تعریف

مثال: قرینه ماتریس عبارت است از   و ملاحظه می شود که

خواص جمع ماتریس ها

الف) جمع ماتریسها خاصیت شرکت پذیری دراد

اثبات: فرض کنید   و   و   سه ماتریس هم مرتبه دلخواه باشند، نشان می دهیم

(A+B)+C=A+(B+C)

قبل از اثبات لازم است معنی عبارات (A+B)+C و A+(B+C) را بدانیم. در این مورد از تعبیر عمل جمع به مثابه عمل یک ماشین کمک می گیریم. از آنجا که ماشین جمع دو ورودی دارد نمی توان یکباره سه ماتریس را با هم جمع کرد، از این رو برای جمع سه   ماتریس A و B و C می توان ابتدا A و B را به ماشین داده و A+B را به دست آورد. سپس A+B و C را به ماشین می دهیم تا (A+B)+Cبه دست آید.

عبارت A+(B+C) به این معناست که نخست B و C را وارد ماشین کرده ایم و B+C را به دست آورده ایم و سپس (B+C)+A را بیرون می دهد.

حال می خواهیم نشان دهیم که در هر صورت ماتریس های بدست آمده مساویند برای این کار قرار می دهیم

درایه سطر I ام ماتریس =D+C درایه سطر I ام ستون j ام ماتریس (A+B)+C

ب) ماتریس صفر عضو بی اثر مجموعه ماتریس ها نسبت به عمل جمع است.

اثبات: فرض کنید   یک ماتریس دلخواه باشد، نشان می دهیم.

که در آن ماتریس صفر هم مرتبه با A است.

اثبات مشابه اثبات فوق است.

ج) هر ماتریس نسبت به عمل جمع دارای متقابل است.

دیدیم که قریبنه هر ماتریس A=[aij]، ماتریسی هم مرتبه با آن به صورت –A[-aij] است. در واقع –A متقابل A نسبت به عمل جمع است، زیرا قبلاً نشان دادیم

که در آن ماتریس صفر هم مرتبه با A است.

د) جمع ماتریس ها دارای خاصیت جابه جایی است.

یعنی اگر A و B دو ماتریس دلخواه هم مرتبه باشند، داریم    A+B=B+A

اثبات:

تعریف ماتریس ها: فرض کنید A و B دو ماتریس هم مرتبه باشند، A-B به صورت زیر تعریف می شود

A-B=A+(-B)

از تعریف فوق نتیجه می گیریم برای اینکه با ماشین جمع، A-B را به دست آوریم، نخست ماشینی با یک ورودی و یک خروجی می سازیم تا هر ماتریسی به آن دهیم آن ماتریس را قرینه کند. حال با دادن ماتریس B به این ماشین، -B از آن خارج می شود.

سپس، A و –B را به ماشین جمع می دهیم تا A+(-B) یعنی A-B را بیرون دهد.

مقایسه خواص جمع ماتریس ها با خواص جمع اعداد حقیقی:

اگر به خواص ماتریس ها توجه کنیم ملاحظه می کنیم که این خواص همانند خواص جمع اعداد حقیقی است، حال می خواهیم ببینیم کدامیکی از خواص دیگر مجموعه اعداد حقیقی با عمل جمع در مجموعة ماتریس ها با عمل جمع برقرار است. می دانیم برای حل معادله a+x=b در مجموعه اعداد حقیقی باید به طریقی a را از طرف اول معادله حذف کرد. بنابراین، طرفین معادله را با –a جمع می کنیم، در اینصورت:

(-a)+ (a+x)=-a+b

با استفاده از خاصیت جابجایی و شرکت پذیری جمع داریم:

(-a+a) +x=b-a)

در نتیجه +x=b-a0 یعنی x=b-a0 این شیوه را می توان برای حل معادله A+X=B در مجموعه ی ماتریس ها نیز به کار برد و گزاره زیر را به دست آورد.

گزاره: اگر A و B دو ماتریس هم مرتبه باشند، در این صورت معادله A+X=B دارای جواب منحصر به فرد X=A-B است.

یکی دیگر از خواص مجموعه اعداد حقیق با عمل جمع، قانون حذف است. یعنی اگر a+x=a+y در این صورت می توان نتیجه گرفت x=y این خاصیت نیز در مورد ماتریس ها با عمل جمع وجود دارد.

قانون حذف در جمع ماتریس ها برقرار است

اثبات: روش اول، فرض کنید A و B و C سه ماتریس هم مرتبه باشند، نشان می دهیم

A+B=A+Cà B=C

طرفین تساوی A+B=A+C را با –A جمع می کنیم با توجه با خاصیت شرکت پذیری و خاصیت ماتریس صفر نتیجه می شود B=C

روش دوم: چون A+B=A+C پس

درایه iام ستون jام =A+C درایه سطر iام ستون jام A+B

تذکر: برای اثبات قانون حرف دو روش مختلف ارائه دادیم. در روش اول، از خواص جمع ماتریسها یعنی شرکت پذیری، عضو بی اثر و… استفاده کردیم، یعنی همان روشی که برای اعداد حقیقی می توان به کار برد. اما در روش دوم ویژگی های ماتریس نقش اصلی را ایفا می کند. در واقع در مورد روش اول برای ما مهم نیست A و B و C ماتریس هستند یا عدد حقیقی و یا هر چیز دیگر، در مورد هر دسته ای از اشیا که دارای خواص جمع ماتریس ها باشند، می توانیم این شیوه را به کار ببریم و این همان رسالت جبر مدرن است که با اصل موضوعی کردن، قضایای مشابه را به یکباره ثابت می کند. زیرا شیوه و روش اثبات قضیه در هر جایی که این اصول صدق می کنند، معتبر است.

ضرب یک عدد (اسکالر) در ماتریس

تعریف: فرض کنید   ماتریسی از مرتبه m*n و r یک عدد حقیقی باشد. از ضرب عدد حقیقی r در A ماتریسی به دست می آید که آن را به صورت rA نمایش می دهیم و به صورت زیر تعریف می شود.

بنابراین (درایه سطر iام ستون jام ماتریس =r.(A درایه سطر iام ستون j ام ماتریس (rA)

مثال: اگر در این صورت

خواص ضرب عدد در ماتریس:

1)فرض کنید r و s دو عدد حقیقی و A یک ماتریس m*n باشد در این صورت داریم

r(sA)=(rs)A

2)اگر r و s دو عدد حقیقی و A یک ماتریس m*n باشد در این صورت داریم

(r+s)A=rA+sA

3)اگر r یک عدد حقیقی و A و B دو ماتریس m*nباشند در این صورت

r(A+B)=rA+rB

4)اگر r یک عدد حقیقی ناصفر و A وB دو ماتریس دلخواه m*n باشند در این صورت

rA=rBà A=B

ضرب ماتریس ها و خواص آن

ضرب ماتریس سطری در ماتریس ستونی

تعریف: ماتریس سطری    و ماتریس ستونی

را در نظر می گیریم حاصل ضرب A در B به صورت زیر تعریف می شود.

با توجه به تعریف فوق حاصل ضرب یک ماتریس سطری در ماتریس ستونی یک عدد حقیقی است که برای به دست آوردن آن به صورت زیر عمل می کنیم.

مثال:

ضرب ماتریس ها در حالت کلی:

تعریف: اگر     و   دو ماتریس مخصوص باشند در این صورت حاصل ضرب AB ماتریسی است m*p که اگر آن را با C نشان دهیم داریم

ملاحظاتی در مورد ضرب دو ماتریس

1-ضرب ماتریسی AB در صورتی تعریف شده است که تعداد ستون های ماتریس اولی، یعنی A با تعداد سطرهای ماتریس دومی، یعنی B، برابر باشد. در این صورت گویند ماتریس A در ماتریس B قابل ضرب است.

2-اگر AB=C برای به دست آوردن هر یک از درایه های ماتریس C به نمحلی که درایه واقع است توجه می کنیم. مثلاً برای بدست آوردن 12C سطر اول A را در ستون دوم B، طبق ضرب یک ماتریس سطری در ماتریس ستونی ضرب می کنیم، و به همین ترتیب

ستون پنجم ماتریس B× سطر سوم ماتریس A = 35C

اگر 1R و 2R و 3R به ترتیب نمایشگر سطر اول و سطر دوم و سوم ماتریس 2×3A و 1C و 2C و 3C نمایشگر ستون اول ، دوم و سوم ماتریس 3×2B باشند. در این صورت AB ماتریسی 2×2 به صورت زیر است.

که در آن، برای مثال، 2C1R حاصل ضرب سطر اول A در ستون دوم B را نشان می دهد.

ماتریس واحد (همانی)

ماتریس واحد، ماتریس مربعی است که تمام درایه های قطر اصلی آن 1 و سایر درایه های صفر است.برای مثال ماتریس واحد 2×2 که با نماد 2I نمایش می دهیم به عبارت است از

به همین ترتیب ماتریس واحد 3×3 عبارت است از

تذکر: ماتریس I را از اینرو، واحد گویند که رفتاری شبیه عدد 1 در ضرب اعداد دارد و چون روی هر ماتریسی (قابل ضرب با آن) اثر کند همان ماتریس را می دهد بنابراین آن را ماتریس همانی نیز می گویند.

گزاره: اگر در ماتریس A سطر دوم صفر باشد و B ماتریسی باشد که AB تعریف شده باشد، در این صورت سطر دوم AB نیز صفر است.

اثبات: قرار می دهیم AB=C درایه های سطر دوم AB از ضرب سطر دوم A در ستون های B به دست می آید. فرض کنید Cijدرایه دلخواهی از سطر دوم AB باشد، بنابراین

به طور کلی، اگر در ماتریس A سطر iام صفر باشد در این صورت سطر I ام ماتریس AB صفر است. به طریق مشابه می توان ثابت کرد.

گزاره: اگر در ماتریس B ستون jام صفر باشد و A ماتریسی باشد که AB تعریف شده باشد، در این صورت ستون jام ماتریس AB صفر است.

بررسی خاصیت جابه جایی در ضرب ماتریسها:

دو ماتریس A و B مفروضند. AB وقتی تعریف شده است که تعداد ستونهای A با تعداد سطرهای B مساوی باشد. مثلاً داشته باشیم و   اگر m و p مساوی نباشد، BA تعریف نشده است. برای اینکه BA تعریف شده باشد لازم است که p=m، یعنی B ماتریس n*m باشد. در اینصورت AB از مرتبه m*m و BA ماتریسی است از مرتبه n*m. حال اگر بخواهیم AB و BA هر دو موجود و هم مرتبه باشند می بایست A و B هر دو ماتریس های مربع و هم مرتبه باشند. اما در این حالت نیز ممکن است BA و AB مساوی نباشد. به مثال زیر توجه کنید.

مثال: اگر         در اینصورت

ملاحظه می شود که AB و BA مساوی نیستند. مثال فوق بیانگر آن است که ضرب ماتریس ها دارای خاصیت جابه جایی نیست. حال به مثال زیر توجه کنید.

مثال: اگر      در این صورت

یعنی AB=BA

ماتریس های تعویض پذیر:

تعریف: اگر A و B دو ماتریس مربع باشند به طوری که AB=BA در این صورت A و B را تعویض پذیر گوییم و یا گوییم A و B با یکدیگر جابجا می شوند.

مثال: دو ماتریس   و   تعویض پذیرند. زیرا

یک خاصیت غیر منتظره در ماتریسها:

می دانیم که مجموعه اعداد حقیقی دارای این خاصیت است که : «حاصلضرب دو عدد حقیقی ناصفر، عددی حقیقی ناصفر است.»

اما در مورد ماتریسها چنین نیست. به مثال زیر توجه کنید. دو ماتریس غیر صفر را در نظر بگیرید. داریم:

ملاحظه می شود که ماتریس هایی مانند A و B وجود دارند به طوری که و   ولی این نوع ماتریس ها را مقسوم علیه صفر می گویند.

تعریف: فرض کنید A یک ماتریس مربع باشد. اگر ماتریس ناصفری مانند B بتوان یافت به طوری    یا در این صورت A را مقسوم علیه صفر گویند.

مثال: ماتریس   مقسوم علیه صفر است زیرا

توانهای طبیعی یک ماتریس مربع:

فرض کنید A یک ماتریس m*n باشد. برای آنکه AA وجود داشته باشد می بایست m=n ، یعنی در صورتی AA تعریف شده است که A ماتریسی مربع باشد. در این صورت AA را با 2A نمایش می دهند.

تعریف: اگر A یک ماتریس مربع باشد، در این صورت توان های طبیعی A به صورت زیر تعریف می شوند

=A1A و =AA2A و 2=AA3A وبا استقرا

An+1 = AAn

در صورتی که A یک ماتریس مربع مرتبه n باشد توان صفر A نیز به صورت زیر تعریف می وشد.

که در آن In ماتریس واحد مرتبه n است.

ماتریس های بالا مثلثی

ماتریس مربعی   را بال مثلثی می نامند هرگاه

Aij     I>j     à aij=0

یعنی، در یک ماتریس بالا مثلثی کلیه درایه های واقع در پایین قطر اصلی صفرند. برای مثال یک ماتریس بالا مثلثی 3×3 در حالت کلی به صورت زیر است

این ماتریس ها را به صورت زیر نشان می دهند

همانطور که از نامگذاری این نوع ماتریس ها معلوم است، در هر ماتریس بالا مثلثی، درایه های واقع بر قطر اصلی و بالای قطر اولی مشخص کننده ماتریس هستند. زیرا تمام درایه های پایین قطر اصلی صفرند.

مثال: ماتریس مربع و صفر ماتریس واحد، بالا مثلث اند.

ماتریس های پایین مثلثی

ماتریس مربع A=[aij] را پایین مثلثی نامند هرگاه

یعنی،  در یک ماتریس پایین مثلثی، همه درایه های واقع در بالای قطر اصلی، صفرند.

مثال: ماتریس روبه رو یک ماتریس

پایین مثلثی 3×3 است. گاهی برای سهولت این ماتریس را به صورت زیر هم نشان می دهند.

نماد O در بالای قطر اصلی به معنای آن است که تمام درایه های بالای قطر اصلی صفرند. نامگذاری این نوع ماتریس ها همانند قبل، بر این اساس استوار است که در ماتریس های پایین مثلثی درایه های واقع بر قطر اصلی ، مشخص کننده ماتریس هتسند.

مثال: ماتریس مربع صفر و ماتریس واحد پایین مثلثی نیز هستند.

ماتریس های قطری:

ماتریع مربع D=[dij] را قطری می نامند، هر گاه هم بالا مثلثی و هم پایین مثلثی باشد، یعنی در یک ماتریس قطری، درایه های پایین و بالای قطر اصلی همگی صفرند، به عبارت دیگر، D قری است هرگاه

بنابراین، ماتریس قطری D به صورت زیر نوشته می شود.

برای سهولت این ماتریس را به صورت زیر هم نشان می دهند.

همانطور که از نام این نوع ماتریس ها بر می آید، در یک ماتریس قطری فقط درایه های واقع بر قطر اصلی مشخص کننده ماتریس اند، برای همین ماتریس قطری را به صورت

diaj(d11 , d12 , dnn)

نیز نشان می دهند.

مثال: ماتریس   قطری است که به صورت(2- و 3 و2) D=diag  نیز می توانیم آن را بنویسیم.

ماتریس واحد (همانی)

ماتریس واحد، ماتریس اسکالری (آن دسته از ماتریس های قطری را که همه درایه های واقع بر قطر اصلی آنها مساویند، ماتریس اسکالر نامند) است که درایه های واقع بر قطر اصلی آن همگی مساوی 1 است. ماتریس واحد مرتبه n را با In نشان می دهند.

مثال: ماتریس واحد 3×3 عبارت است از

وقتی مرتبه ماتریس واحد معلوم باشد و یا اهمیت نداشته باشد، ماتریس واحد را با I نشان می دهند و برای هر ماتریس مرتبه n مانند A داریم     InA=AIn=A

یعنی، ماتریس واحد، عضو بی اثر مجموعه ماتریس های مربع نسبت به عمل ضرب است. برای همینن ماتریس واحد رفتاری شبیه عدد یک در ضرب اعداد دارد.

و به سادگی دیده می شود که برای هر عدد طبیعی K داریم:       IK=I

مثال: هر ماتریس اسکالر مضربی از ماتریس واحد است. یعنی؛

ماتریس های خود توان

ماتریس مربع A را خودتوان می نامند هرگاه =A2A

 مثال: ماتریس  خودتوان است زیرا؛

گزاره: اگر A خودتوان باشد، در این صورت برای هر عدد طبیعی n، داریم:

An=A

ماتریس های پوچ توان:

ماتریس مربع A را پوچ توان نامند هرگاه به ازای یک عدد طبیعی، مانند n، داشته باشیم

بدیهی است که اگر  به ازای هر عدد طبیعی بزرگتر از n مانند m داریم

کوچکترین این n ها را اندیس پوچ توانی A گویند.

زیرماتریس ها وافراز کردن

یک زیر ماتریس یک ماتریس مفروض A ماتریسی است که از حذف تعدادی از سطرها یا ستون های ماتریس A بدست آمده باشد، برای مثال اگر

در این صورت هر یک از ماتریسهای زیر یک زیر ماتریس A می باشند.

زیر ماتریس     از حذف سطرهای اول و دوم و ستونهای اول و سوم، و زیر ماتریس ]4   3  2 [ از حذف سطرهای دوم و سوم و چهارم و ستون اول به دست می آیند.

هرگاه با ترسیم خطوط افقی و عمودی بین سطرها و ستونهای یک ماتریس آن را تقسیم بندی کنیم، گوییم ماتریس را افراز کرده ایم. با تغییر این خطوط افرازهای متفاوتی از یک ماتریس ساخته می شود. مثلاً

دو افراز مختلف از ماتریس A می باشند.

وقتی ماتریس ها از ظرفیت حافظه کامپیوتر بزرگترند، از ماتریس های افراز شده استفاده فراوان می کنند. مثلاً در ضرب دو ماتریس افراز شده، می توان ماتریس ها را روی دیسک نگه داشت. و فقط زیر ماتریس هایی را که در تشکیل حاصل ضربهای زیر ماتریسی لازمند در حافظه آورد. معلوم است که افراز باید به قسمی صورت گیرد که حاصل ضرب ماتریسهای نظیر قابل تعریف باشد.

فرض کنید A و B ماتریسیهایی باشند که AB تعریف شده باشد حال اگر A و B را به صورت

افزار کرده باشیم در این صورت به آسانی ثابت می شودکه برای محاسبه ماتریس AB می توان C و D و… را شبیه درایه ها تصور کرد و عمل ضرب را انجام داد، بنابراین

&nb